GUÍA PARA EL EXAMEN BIMESTRAL

CONVOCATORIA PARA LA DEMOSTRACIÓN CONCURSO DEL TEMA 923.- TESELADOS Y MOSAICOS

La maestra Madeleine Palma Ocampo, maestra de Matemáticas de la Escuela Secundaria “Antonio Caso”, de Iguala, Gro.

CONVOCA

A los alumnos de los terceros A, C, D, y E, de la misma institución y a los cuales imparte la asignatura mencionada a participar en la demostración - concurso individual,

Diseño Creativo de Teselados y Mosaicos 2015.

BASES

LUGAR Y FECHA:

œ   La demostración concurso se llevará a cabo el día lunes 7 de diciembre en punto de las 12:30 horas en la cancha techada de la institución.

CARACTERÍSTICAS:

œ   Desarrollarán un diseño geométrico basado en las técnicas analizadas en los temas 922 y 923, del bloque 2.

œ   Trazarán o armarán un teselado o mosaico con al menos una técnica de trasformación en el plano, Simetría Axial, Traslación o cualquier tipo de Rotación.

œ   Dicho diseño podrá ser trazado o en relieve, éste último, siempre y cuando no implique el uso de navajas o cúter.

œ   Puede basarse en los ejemplos, pero no copiarlos, es decir deben ser originales

œ   Estar elaborados con material reciclable, (todo tipo de papel, cartón, tetrapac, poli papel, revistas, panfletos de papel, cajas, colores, etc.)

œ   Evitar el uso de unicel, aluminio en papel y en lata, foami, diamantina en polvo, clavos, alambres, CD, popotes, pintura en espray, o de aceite, o cualquiera que implique el uso de solventes).

œ   Todos los trabajos deberán tener una ficha descriptiva en la parte de atrás del trabajo y por ningún motivo deberá verse el nombre del alumno o alumna.

PREMIOS

œ   La maestra Madeleine Palma Ocampo premiará los tres mejores trabajos elegidos por el jurado, todos como primer lugar y recibirán el mismo premio.

NOTA: LA DECISIÓN DEL JURADO ES INAPELABLE, LAS INCIDENCIAS SERÁN RESUELTAS POR LA ACADEMIA DE MATEMÁTICAS.

FICHA DESCRIPTIVA PARA EL PROYECTO

FICHA

DE TESELADOS Y MOSAICOS

• NOMBRE COMPLETO
• GRADO
• GRUPO
• TÉCNICA O TÉCNICAS USADAS

DESCRIPCIÓN

1. Anotar todo lo que hiciste para desarrollar tu proyecto, 

.- cantidad de material

.- tipo de material

.- con que se unió o pegó

.- por qué eligió esa técnica

.- figuras

.- tamaños

.- etc.

2.- Las técnicas libres solo son decorativas, no deben opacar las geométricas

3.- Utilizar al menos una de las que vimos en clase, aunque también de las analizadas en los videos son válidas, solo describirlas y fundamentarlas.

Rotación.- figuras

ROTACIÓN POR UN ANGULO

ACTIVIDADES, EJEMPLOS, PRACTICAS, DISEÑOS

LOS DISEÑOS DEBEN SER PERSONALES

PERO TODAVÍA GEOMÉTRICOS

ES DECIR CON EQUIPO DE GEOMETRÍA

ejemplos y prácticas
son del tema 922
simetría axial

ejemplo y practica de traslación

del tema 922

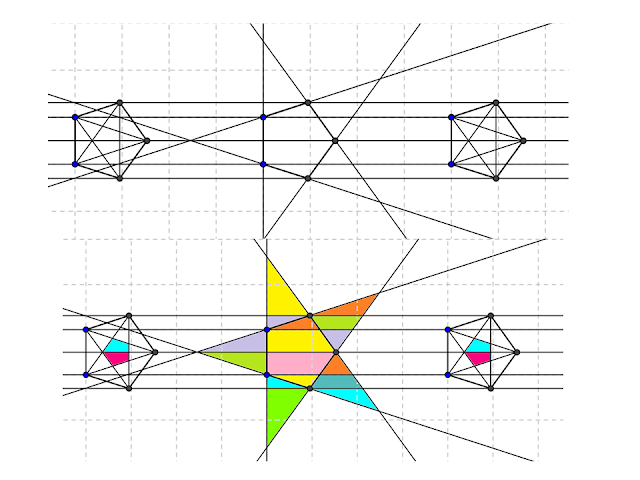
actividades del tema 923

primero la simetría axial

posterior el diseño

primero la traslación de un  pentágono a la misa distancia

posterior diseño

Contenido 9.2.3..- Construcción de diseños que combinan la Simetría Axial, Traslación y Rotación

Aprendizaje Esperado: Explica el tipo de transformación (reflexión, rotación o traslación) que se aplica a una figura para obtener la figura transformada. Identifica las propiedades que se conservan.

CONOCIMIENTOS PREVIOS

Identifica los tres tipos de trasformaciones en el plano (traslaciones, rotaciones simetría axial). Analizados en el contenido anterior.

ACTIVIDADES

Después de haber realizado las actividades, se realizará un diseño sencillo

serán dos evaluaciones, la primera por el trazo, la segunda por el diseño

EJEMPLOS Y PRACTICAS

LOS EJEMPLOS DE SIMETRÍA AXIAL Y TRASLACIÓN SON UNA FIRMA

LAS PRÁCTICAS DE SIMETRÍA AXIAL Y TRASLACIÓN SON EVALUACIÓN

Contenido: 9.2.2 Análisis de las propiedades de la rotación y de la traslación de figuras.

Eje. Forma Espacio y Medida

Tema. Figuras y Cuerpos

Aprendizaje Esperado: Explica el tipo de transformación (reflexión, rotación o traslación) que se aplica a una figura para obtener la figura transformada. Identifica las propiedades que se conservan.

En este video se observan otras técnicas de teselados y mosaicos

https://www.youtube.com/watch?v=gz3O89wWa9I

CONOCIMIENTOS PREVIOS

Conceptualización de los movimientos en el plano

SIMETRÍA AXIAL.- La simetría axial se da cuando los puntos de una figura coinciden con los puntos de otra, al tomar como referencia una línea que se conoce con el nombre de eje de simetría.

Puede observarse que en la imagen no se conserva la orientación (la derecha se convierte en izquierda y la izquierda en derecha).

En la simetría axial se da el mismo fenómeno que en una imagen reflejada en el espejo.

TRASLACIÓN.- En geometría, una traslación es una isometría en el espacio euclídeo caracterizada por un vector , tal que, a cada punto P de un objeto o figura se le hace corresponder otro punto P'

Las traslaciones pueden entenderse como movimientos directos sin cambios de orientación, es decir, mantienen la forma y el tamaño de las figuras u objetos trasladados, a las cuales deslizan según el vector. Dado el carácter de isometría para cualquier punto P y Q se cumple la siguiente identidad entre distancias

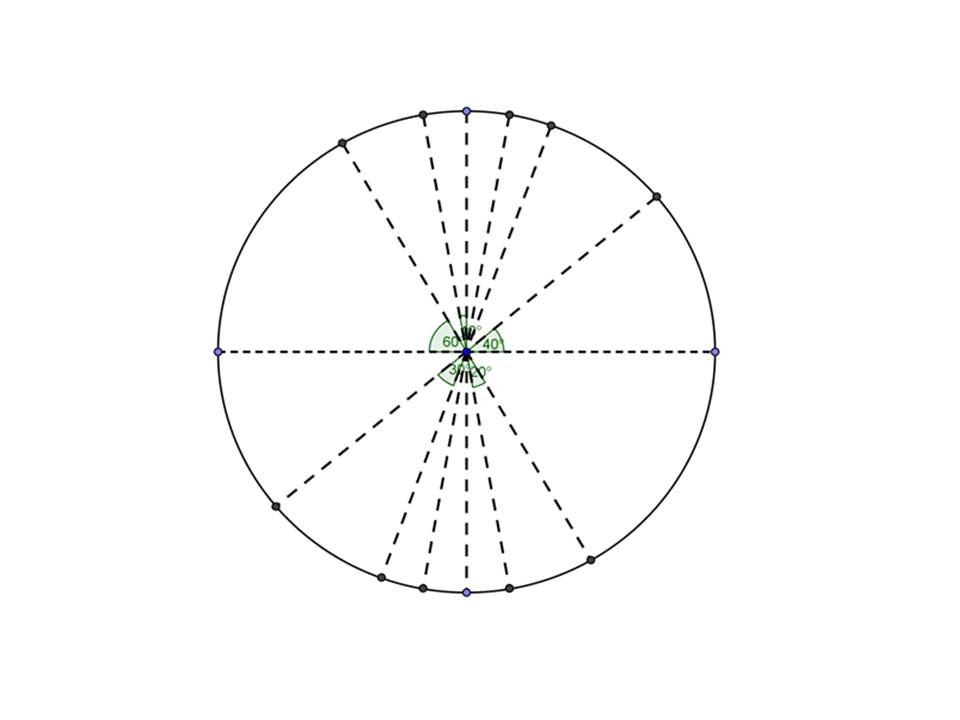
ROTACIÓN CENTRAL.- Este tipo de movimiento en el plano, también es llamado simetría central, el centro es el eje de rotación, o centro de simetría, donde las figuras rotan

ROTACIÓN POR UN ÁNGULO.- 

EVALUACIÓN DEL LIBRO

TAREA EN EL LIBRO

Cuadro de la actividad 7 de la página 81

Forma general	Forma factorizada	Soluciones
x2 + 7x + 12 = 0	(x + 4)(x + 3) = 0	x1 = - 4           x2   - 3
x2 + 8x + 15 = 0	(x + 3)(x + 5) = 0	x1 = - 3            x2   - 5
x2 + 5x + 6 = 0	(x + 2)(x + 3) = 0	x1 = - 3            x2   - 2
x2 + 14x + 45 = 0	(x + 9)(x + 5) = 0	x1 = - 9            x2   - 5
x2 + 4x + 3 = 0	(x + 3)(x + 1) = 0	x1 = - 3            x2   - 1

Tabla de la actividad 2 de la página 82

Forma general	Forma factorizada	¿Cómo son los números buscados?
x2 - x - 2 = 0	(x - 2)(x + 1) = 0	Sumados dan -1, multiplicados dan –2.
x2 + 7x + 10 = 0	(x + 2)(x + 5) = 0	Sumados dan +7, multiplicados dan +10.
x2 + x - 12 = 0	(x + 4)(x - 3) = 0	Sumados dan +1, multiplicados dan -12
x2 + 2x - 3 = 0	(x + 3)(x - 1) = 0	Sumados dan +2, multiplicados dan –3.
x2 - 7x + 12 = 0	(x - 4)(x + 3) = 0	Sumados dan  -7, multiplicados dan +12

TAREA.- Resolver los incisos a, b, c y d, de la página 82 del libro

EJERCICIO Y EVALUACIÓN

CONCEPTUALIZACIÓN

Si al solucionar las factorizaciones los resultados son.

Cero, tiene una solución

Un número positivo, tienen dos soluciones

Un número negativo, tiene una solución

a)    4x² + 6x = 0

b)    5x² + 10x = 0

c)    x² + 4x = 7x

d)   x² + 6x +8 = 0

PROCEDIMIENTOS

9.2.1 Uso de ecuaciones cuadráticas para modelar situaciones y resolverlas usando la factorización.

Eje. Sentido Numérico y Pensamiento Algebraico

Tema. Patrones y ecuaciones

Intención Didácticas: Que los alumnos usen la factorización al resolver problemas y ecuaciones de la forma ax²+bx=0.

Estándar: Resuelve problemas que involucran el uso de ecuaciones lineales o cuadráticas.

Aprendizaje Esperado: Resuelve problemas que implican el uso de ecuaciones de segundo grado 

Indicador de Desempeño: Resuelve ecuaciones de segundo grado mediante la factorización

CONOCIMIENTOS PREVIOS

Consigna: Organizados en equipos resuelvan los siguientes problemas.

1.    El área de un cuadrado es igual a 8 veces la medida de su lado. ¿Cuánto mide por lado el cuadrado?

2.    El triple del área de un cuadrado menos seis veces la medida de su lado es igual a cero. ¿Cuánto mide por lado el cuadrado?

BLOQUE II

COMPETENCIAS

• RESOLVER PROBLEMAS QUE IMPLIQUEN ECUACIONES DE SEGUNDO GRADO, MEDIANTE PROCEDIMIENTOS PERSONALES Y/O CANÓNICOS, FACTORIZAR
• UTILIZAR LA SEMEJANZA DE LOS TRIÁNGULOS PARA RESOLVER PROBLEMAS
• PROBABILIDAD POR SIMULACIÓN

CONVOCATORIA DEL CONCURSO EN EL FACE

BASES

1.- PODRÁN PARTICIPAR SOLO LOS EQUIPOS DE 3° A, C, D , E, DE LA ESC. SEC. ANTONIO CASO, QUE PRESENTARON ARBOLES GRÁFICOS LOS DÍAS JUEVES Y VIERNES 5 Y 6 DE NOVIEMBRE DE 2015.

2.- LAS FOTOS SERÁN PUBLICADAS EN EL PERFIL DE LA MAESTRA MADELEINE PALMA OCAMPO, LA RESPONSABLE DE LOS GRUPOS Y LA MATERIA DE MATEMÁTCAS.

3.- SE COMPARTIRÁN EN EL FACE OFICIAL DE LA SECUNDARIA Y SOLO PODRÁN DAR UN LIKE, DURANTE 48 HORAS A PARTIR DE LA PUBLICACIÓN DE LAS IMÁGENES

RASGOS A EVALUAR EN EL ARBOL

1.- QUE ESTE ELABORADO CON MATERIAL RECICLABLE

2.- ORIGINALIDAD

3.- QUE SU ELABORACIÓN SEA ECONÓMICA

4.- QUE SE PUEDA REPRODUCIR O REELABORAR CON FACILIDAD

TERMINADO EL TIEMPO GANARÁ EL ARBOL CON MAS LIKES, SIEMPRE Y CUANDO CUMPLA CON LOS RASGOS, LA DECISIÓN FINAL SERÁ TOMADA POR LA MAESTRA MADELEINE PALMA OCAMPO EN CASO DE CUMPLIRSE CON LAS BASES.

PRESENTACIÓN.- ÁRBOL GRÁFICO DE MADELEIN

EN EL ÁRBOL COLGARÁN LA TABLA Y LAS GRÁFICAS

Y UN PERSONIFICADOR CON EL NOMBRE DEL EQUIPO

PROYECTO

1.- Diseñar la encuesta: EJEMPLO:

Encuesta aplicada a 20 alumnos de diferentes grupos de la Escuela Secundaria "Antonio Caso", de la ciudad de Iguala, Gro., Mex., el 3 de noviembre de 2015

2.- Plantear la pregunta: EJEMPLO:

De las siguientes acciones ¿cuál te gustaría que tu maestra de matemáticas modificara?

1.- la forma de enseñar

2.- la forma de planear

3.- la forma de evaluar

Todas en una tabla como te lo indicarán el clase

3.- Llevar a cabo la presentación, por medio de gráficos

Cada una de ellas cabe en un cuarto de hoja y se colgarán en un arbolito que pueden elaborar de papel, cartón, revistas, periódico, ramas secas, o que tengan en casa

Para graficar

9.1.7 Diseño de una encuesta o un experimento e identificación de la población en estudio. Discusión sobre las formas de elegir el muestreo. Obtención de datos de una muestra y búsqueda de herramientas convenientes para su presentación.

Aprendizaje esperado.-Calcula y explica el significado del rango y la desviación media.

CONOCIMIENTOS PREVIOS

œ    Realizar un recordatorio sobre los diferentes tipos de gráficas que se han analizado en los dos grados anteriores.

Ø    Planear por binas la forma para recabar datos y representarlos por medio de un álbum de gráficas

GRÁFICAS.- Representaciones gráficas de los resultados que se muestran en una tabla estadística. Pueden ser de formas muy diversas, pero con cada tipo de gráfica se cumple un propósito. Por ejemplo, en los medios de comunicación, libros de divulgación y revistas especializadas se encuentran multitud de gráficas estadísticas en las que, con notable expresividad, se ponen de manifiesto los rasgos de la distribución que se pretende destacar. Los diagramas de barras, los diagramas de sectores, los histogramas y los polígonos de frecuencias son algunas de ellas.

Ø    Barras.- En este tipo de gráfica, sobre los valores de las variables se levantan barras estrechas de longitudes proporcionales a las frecuencias correspondientes. Se utilizan para representar variables cuantitativas discretas.

Ø    Histograma.- Los histogramas se utilizan para representar tablas de frecuencias con datos agrupados en intervalos. Si los intervalos son todos iguales, cada uno de ellos es la base de un rectángulo cuya altura es proporcional a la frecuencia correspondiente.

Ø    Poligonal.- Si se representan las frecuencias acumuladas de una tabla de datos agrupados se obtiene el histograma de frecuencias acumuladas o su correspondiente polígono.

Ø    Sectorial.- En un diagrama de este tipo, los 360º de un círculo se reparten proporcionalmente a las frecuencias de los distintos valores de la variable. Resultan muy adecuados cuando hay pocos valores, o bien cuando el carácter que se estudia es cualitativo.

Ø    Pictograma.- Gráfica que representa valores por medio de dibujos, cada uno de ellos representa una cantidad determinada.

Rango es el intervalo entre el valor máximo y el valor mínimo; por ello, comparte unidades con los datos. Permite obtener una idea de la dispersión de los datos, cuanto mayor es el rango, más dispersos están los datos de un conjunto


En estadística la desviación absoluta promedio o, sencillamente desviación media o promedio de un conjunto de datos es la media de las desviaciones absolutas y es un resumen de la dispersión estadística. ...también llamada dispersión.

Las medidas de dispersión, también llamadas medidas de variabilidad, muestran la variabilidad de una distribución, indicando por medio de un número si las diferentes puntuaciones de una variable están muy alejadas de la media. Cuanto mayor sea ese valor, mayor será la variabilidad, y cuanto menor sea, más homogénea será a la media. Así se sabe si todos los casos son parecidos o varían mucho entre ellos.

Para calcular la variabilidad que una distribución tiene respecto de su media, se calcula la media de las desviaciones de las puntuaciones respecto a la media aritmética. Pero la suma de las desviaciones es siempre cero, así que se adoptan dos clases de estrategias para salvar este problema. Una es tomando las desviaciones en valor absoluto (desviación media) y otra es tomando las desviaciones al cuadrado (varianza).

EXPERIMENTO 3.- LANZAR DOS DADOS

EVENTO	RESULTADOS POSIBLES	PROBABILIDAD
A {La suma es dos}
B {La suma es tres}
C {La suma es siete}	6	6/36
D {La suma es diez}
E {La suma es 3 o 10}
F {La suma es mayor que 10 o múltiplo de 4}